Some ideas about the Kalman filter.
Say we have a dynamic system that has the internal state $\textbf{x}$ and the control input $\textbf{u}$. Although we don't know the internal state $\textbf{x}$, we can observe it and have the measurement $\textbf{z}$.
Then how can we estimate the internal state $\textbf{x}$?
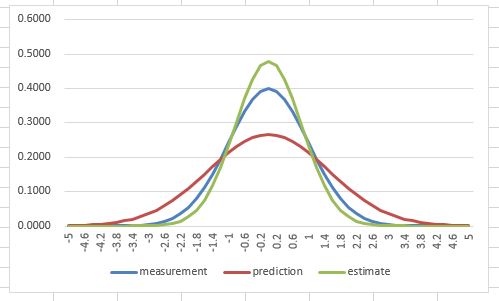
At first, we may have an initial estimated state and the covariance $(\textbf{x}_0^*, \textbf{P}_0^*)$. So we use this to make a prediction based on the dynamics of the system, then we get $({\textbf{x}_1}', {\textbf{P}_1}')$.
At the time $t_1$, we also do a measurement and get $(\textbf{z}_1, \textbf{R}_1)$.
So we use the prediction and the measurement to have an estimation of the internal state at time $t_1$, which is $({\textbf{x}_1^*}, {\textbf{P}_1^*})$.
From the previous examples, we know that finding the weight to make an unbiased estimation is the key such that we can have a minimum of the covariance or variance of the estimation.
The Kalman gain $\textbf{K}$ in the Kalman filter invented by Rudolf E. Kalman can give us a good estimation of the internal state $\textbf{x}$ for a linear system.
We can image $\textbf{K}_1$ is a function of ${\textbf{P}_1}'$ and $\textbf{R}_1$.
By following the wiki:Kalman filter's naming convention,
$\textbf{K}_1={\textbf{P}_1}'\textbf{H}_1^T(\textbf{H}_1{\textbf{P}_1}'\textbf{H}_1^T+\textbf{R}_1)^{-1}$
Such that the $({\textbf{x}_1^*}, {\textbf{P}_1^*})$ is
$\textbf{x}_1^*=(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{x}_1}'+\textbf{K}_1\textbf{z}_1$
$\textbf{P}_1^*=(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{P}_1}'$
So for the estimation of the internal state $\textbf{x}$ at the time $t$:
1. use $({\textbf{x}_{t-1}^*}, {\textbf{P}_{t-1}^*})$ to get a prediction $({\textbf{x}_t}', {\textbf{P}_t}')$.
2. take a measurement at the time $t$ and get $(\textbf{z}_t, \textbf{R}_t)$.
3. calculate $\textbf{K}_t$
4. use $\textbf{K}_t$ to get $({\textbf{x}_t^*}, {\textbf{P}_t^*})$.
The following diagram shows a simple flow chart of the process.