Estimation - Kalman Filter II

From the point of view of the measurement, we can make a prediction of the measurement ${\textbf{z}_1}'$ from ${\textbf{x}_1}'$, and we can get $({\textbf{z}_1}', \textbf{H}_1{\textbf{P}_1}'\textbf{H}_1^T)$.

The measurement is $(\textbf{z}_1, \textbf{R}_1)$, the estimate is

$\textbf{z}_1^* = (\textbf{I}-\textbf{G}_1){\textbf{z}_1}'+\textbf{G}_1\textbf{z}_1$

a good estimate comes with

$\textbf{G}_1=\textbf{H}_1{\textbf{P}_1}'\textbf{H}_1^T(\textbf{H}_1{\textbf{P}_1}'\textbf{H}_1^T+\textbf{R}_1)^{-1} = \textbf{H}_1\textbf{K}_1$

$\textbf{z}_1^* = (\textbf{I}-\textbf{H}_1\textbf{K}_1)\textbf{H}_1{\textbf{x}_1}'+\textbf{H}_1\textbf{K}_1\textbf{z}_1$

$ = \textbf{H}_1(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{x}_1}'+\textbf{H}_1\textbf{K}_1\textbf{z}_1$

$\textbf{H}_1\textbf{x}_1^* = \textbf{H}_1(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{x}_1}'+\textbf{H}_1\textbf{K}_1\textbf{z}_1$

so $\textbf{K}_1$ can give a good estimate for $\textbf{z}_1^*$, it seems also imply that

 $(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{x}_1}'+\textbf{K}_1\textbf{z}_1$ can give a good estimate for $\textbf{x}_1^*$.

Estimation - Probability Distribution

Here is the chart of the probability distribution of a 1D example on the (prediction, measurement, estimate) for the normal distribution case.

As we can see, both the measurement and the prediction are unbiased, but have different probability distributions.  By adjusting the weight, we can find a better unbiased estimation.

Estimation - Kalman Filter

Some ideas about the Kalman filter.

Say we have a dynamic system that has the internal state $\textbf{x}$ and the control input $\textbf{u}$.  Although we don't know the internal state $\textbf{x}$, we can observe it and have the measurement $\textbf{z}$.

Then how can we estimate the internal state $\textbf{x}$?

At first, we may have an initial estimated state and the covariance $(\textbf{x}_0^*, \textbf{P}_0^*)$.  So we use this to make a prediction based on the dynamics of the system, then we  get $({\textbf{x}_1}', {\textbf{P}_1}')$.

At the time $t_1$, we also do a measurement and get $(\textbf{z}_1, \textbf{R}_1)$.

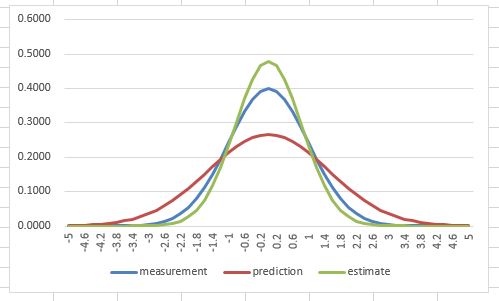
So we use the prediction and the measurement to have an estimation of the internal state at time $t_1$, which is $({\textbf{x}_1^*}, {\textbf{P}_1^*})$.

From the previous examples, we know that finding the weight to make an unbiased estimation is the key such that we can have a minimum of the covariance or variance of the estimation.

The Kalman gain $\textbf{K}$ in the Kalman filter invented by Rudolf E. Kalman can give us a good estimation of the internal state $\textbf{x}$ for a linear system.

We can image $\textbf{K}_1$ is a function of  ${\textbf{P}_1}'$ and $\textbf{R}_1$.

By following the wiki:Kalman filter's naming convention,

$\textbf{K}_1={\textbf{P}_1}'\textbf{H}_1^T(\textbf{H}_1{\textbf{P}_1}'\textbf{H}_1^T+\textbf{R}_1)^{-1}$

Such that the $({\textbf{x}_1^*}, {\textbf{P}_1^*})$ is
$\textbf{x}_1^*=(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{x}_1}'+\textbf{K}_1\textbf{z}_1$
$\textbf{P}_1^*=(\textbf{I}-\textbf{K}_1\textbf{H}_1){\textbf{P}_1}'$

So for the estimation of the internal state $\textbf{x}$ at the time $t$:
1. use  $({\textbf{x}_{t-1}^*}, {\textbf{P}_{t-1}^*})$ to get a prediction $({\textbf{x}_t}', {\textbf{P}_t}')$.
2. take a measurement at the time $t$ and get $(\textbf{z}_t, \textbf{R}_t)$.
3. calculate $\textbf{K}_t$
4. use  $\textbf{K}_t$ to get $({\textbf{x}_t^*}, {\textbf{P}_t^*})$.

The following diagram shows a simple flow chart of the process.

Estimation - Data Fusion

From the previous example, we know if we want to merge two data, we also need the standard deviation or variance of the data in order to make a better estimation.  By following the tradition, we will use variance for the following derivations.

Say the data fusion process is defined as: $d_f = \mathcal{F}(d_1,d_2)$, $d_i = (x_i,\sigma_i^2)$

To have a good estimate means to have an unbiased $x_f$ with minimizing the $\sigma_f^2$ at the same time.

Say $x_f = \alpha_1x_1+\alpha_2x_2$, and $\alpha_1+\alpha_2=1$

Then $\sigma_f^2 = \alpha_1^2\sigma_1^2+\alpha_2^2\sigma_2^2+2\alpha_1\alpha_2\mathcal{C}(d_1,d_2)$, $\mathcal{C}(d_1,d_2)$ is the covariance of the data.

If both data are uncorrelated, $\sigma_f^2 = \alpha_1^2\sigma_1^2+\alpha_2^2\sigma_2^2$

With the uncorrelated case, let $\alpha_2=1-\alpha_1$, and

$ \frac{\partial}{\partial \alpha_1} \sigma_f^2 = 2\alpha_1\sigma_1^2+(2\alpha_1-2)\sigma_2^2=0$

then $\alpha_1 = \sigma_2^2/(\sigma_1^2+\sigma_2^2) $, $\alpha_2 = \sigma_1^2/(\sigma_1^2+\sigma_2^2) $